| True negative | ||
|---|---|---|
| True positive | ||
| False negative | ||
| False positive | ||
| Specificity | \( \equiv \frac{T_n}{T_n+F_p} \) | |
| Sensitivity | \( \equiv \frac{T_P}{T_p+F_n} \) | |
| Prevalence | \( \equiv T_p+F_n \) | |
| Positive predictive value | \( \equiv \frac{T_P}{T_p+F_p} \) | |
| Negative predictive value | \( \equiv \frac{T_n}{T_n+F_n} \) | |
| Positive likelihood ratio | \( \equiv\frac{S_n}{1- S_p} \) | |
| Negative likelihood ratio | \( \equiv\frac{ 1 - S_n }{S_p} \) |

Photo credit to Kendal
The goal of this article is to discuss the two major ways in which binary diagnostic medical testing can be deceptive, particularly in the context of testing for sexually transmitted infections. First, the time delay as the pathogen multiplies in the body creates a window during which a person may be contagious but the infection may be asymptomatic and/or undetectable. Second, no test is perfectly accurate. There are always false positives and false negatives. Understanding the math behind the probability yields some surprising results, particularly for low prevalence diseases.
This article cites little original research. To write a proper literature review on a subject this broad requires a far higher word count and more subject-matter expertise than I have. Therefore, this article cites mostly review articles, peer-reviewed articles that present a subject-matter expert's view of the state of the science.
Articles like this one are extremely frustrating to compose because the data one would like to cite are often not available. For example, the window periods of gonorrhea and chlamydia screening tests are poorly understood. No one has a good study to estimate what the range of the window periods may be. As I pass on to my readers this incomplete data, know that I am deeply sorry for these frustrations and more. I am acutely aware of these shortcomings and have done my best to minimize them.
Prevalence: the number or percent of people in a population currently infected with a disease
Incidence: the number or percent of people in a population with new infections per time (ie 200,000 new infections per year)
Incubation period: the time between exposure and development of symptoms (often highly variable)
Window period: the time between exposure and possible detection with a diagnostic test
Nucleic acid amplification test (NAAT): Diagnostic test which directly detects the pathogen's DNA or RNA in the sample. There are many types of NAAT tests which use different techniques to amplify the DNA/RNA.
Enzyme immunoassay (EIA): Diagnostic test which detects antibodies in the body and proteins in the pathogen. In some literature, this is synonymous with ELISA but in HIV tests ELISAs only detect antibodies and EIAs detect antibodies + an HIV protein, p24.
Enzyme-linked immunosorbent assay (ELISA): Diagnostic test which detects antibodies in the body. ELISA tests give results in minutes. Most diagnostic tests in a doctor's office where they mix a few things on the counter are ELISA tests.
Diagnositic medical tests are always a trade off between expense, time, and accuracy. The cheapest, fastest tests usually have reasonably good sensitivity but poor specificity. Typically such tests are binary classification tests which do not precisely measure the target molecule, they only give a yes/no result depending on whether the target molecule is above a certain threshold. To illustrate, let us look at the different types of pregnancy tests. In detecting pregnancy, we are testing for a protein called human chorionic gonadotropin (hCG). A home pregancy urine test is a binary test; it does not give a measurement, it gives a yes/no result. More expensive lab tests measure the concentration which opens up the possibility of an inconclusive test ("if x < a, negative; if a < x < b, inconclusive; if x > b, positive"). The best lab pregancy tests look at the concentrations of three or four proteins and a more complex algorithm is used to decide if the woman is pregnant and, if so, estimate the date of conception.
The cut-off for a positive home pregnancy urine test is between 6 and 50 mIU/mL hCG [1,2]. An mIU is a milli-International Unit, a unit of measurement which converts to real units of mass or volume differently depending on the substance being measured (seriously, it is a totally arbitrary unit decided by committee for each substance without any consistent application of reason). For hCG, 1 IU = \(6\times 10^{-8} \) g [3], therefore a home pregancy cutoff is between 0.4 and 3 ng/mL of hCG. Obviously the use of International Units reflects poorly on the biology profession since they are completely arbitrary and unnecessary. Like so many things in the nomenclature of biology, they seem to serve no purpose except to make the literature more opaque.
For any test of any infection, there are two delay periods. The time between exposure and presentation of illness is known as the incubation period. The time between exposure and a reliable, positive diagnostic test result is known as the window period. Both delays are things we intuitively know. No one imagines that symptoms develop immediately upon exposure to a pathogen. If a person sexually contracts chlamydia, we rightly imagine that a test one minute after the sex act will not detect the pathogen. However, for most diseases, this window period is larger than we expect. People often say "I was tested on xxxx date, so I did not have anything then" when a more correct formulation of that sentence would be "I was tested on xxxx date, so unless I contracted something within the window period or unless I had a false negative result, I did not have anything then."
Based on lack of available research into this topic, it can be inferred that the medical community is not seriously concerned with measuring the window period of their STD tests. In practice, so long as the window period is not much longer than the incubation period, the test functions well enough for the clinic without thinking about these complications. However, the medical community cares a great deal about bloodborne pathogens and the window periods for those tests because they affect the safety of the blood available for transfusions. Infections via blood transfusion have been known since 1943 [4] when it was documented as a transmission route for hepatitis. HIV infection via blood transfusion was first documented in 1983 [5] in a baby who received a platelet transfusion only two years after the seminal paper on HIV [6]. Until the 1980s, the primary pathogens of concern were the hepatitis viruses. Today, the research is focused on HIV and Hep C.
As a result of transmissions via blood transfusion, the window periods of screening tests for hepatitis B/C and HIV are reasonably well documented. The window period of other STDs are known with far less accuracy and should be taken as cruder estimates.
| Pathogen/test | Window period | Notes |
|---|---|---|
| HIV NAAT | 10-27 days [7] 10-15 [8] | Not commonly used, significantly expensive |
| HIV EIA | 15-30 days [7] <20 days [9] 15-20 [8] <4 weeks [10] | Lab test (no same day results) |
| HIV ELISA | about 22 days [11] | Rapid HIV tests (results in minutes) are ELISA tests |
| Gonorrhea NAAT | 5-14 days [12] <14 days [10] | Clinical best estimate, good data does not currently exist |
| Chlamydia NAAT | 5-14 days [12] up to 5 weeks [13] | Good data does not currently exist, all recommendations are based on incomplete evidence resulting in inconsistent recommendations |
| Syphilis ICS, VDRL, and RPR tests | 7-14 days after blisters or 3 to 4 weeks post-exposure [12] up to 12 weeks [10] |
[Caption] HIV tests come in three flavors each of which is an active area of research and continues to improve. The NAAT is the most expensive, most reliable, and shortest window-period test because it detects viral DNA or RNA. A NAAT test is used when an HIV diagnosis is strongly suspected but not for routine screening. HIV enzyme immunoassay (EIA) tests are used in routine screenings. They are performed in a lab so no results are given on the spot. The EIA test detects antibodies and an antigen from the virus called p24. p24 levels rise quickly after infection and then fall to undetectable levels as antibody levels start to rise. This causes a gap period in the EIA test where p24 levels may be too low to detect as they fall and antibody levels are not yet high enough. A person tested every day after exposure would be negative (p24 too low), positive (p24 detectable), negative (p24 undetectable), and positive again (p24 undetectable but antibodies now detected). The gap period is brief and may not exist for all persons [9]. Enzyme-linked immunosorbent assays (ELISA) are used in a doctor's office to screen for a variety of diseases including HIV. ELISA tests are the most economical and least specific tests available. Because it only detects antibodies, the window period is longer for ELISA tests than for NAAT or EIA tests. In the US, the most common tests for gonorrhea or chlamydia are types of NAAT tests. The window periods of these tests are so poorly understood that clinicians write open letters to medical journals calling for better research to guide their decisions [13]. Trichomoniasis and herpes are not on this table. Trichomoniasis can be tested for using a cell culture, wet slide microscopy, NAAT, or antigen test. Most US labs use a NAAT test for trichomoniasis. I cannot find data on the window period of any trichomoniasis test. Herpes viruses (HSV-1 and HSV-2) are difficult to test for and usually of low clinical consequence (except in the case of pregnant women or infants) so little effort has been made to screen for those viruses.
Binary classification is the process of converting information to a yes/no or positive/negative result. Although it is the simpliest type of classification test, it is deceptively complicated. Any binary classification is capable of returning four possible results: true positive or true negative (the test was right), and false positive or false negative (the test was wrong). These results are typically displayed in a chart shown below known as a "confusion matrix". To evaluate a test's performance, we rely on metrics that tell us something about the conditional probabilities of certain results. As of today, the Wikipedia article Evaluation of binary classifiers has 14 such metrics. Each of them has applicability in certain situations. They are all commonly misinterpreted in situations where they do not apply as well. Of those 14, two of them are commonly reported for medical tests (sensitivity/specificity) and two others are of interest to the clinician and the patient (positive and negative predictive values, PPV/NPV). Because we are interested in PPV and NPV, but medical device companies report sensitivity and specificity, we are going to have to solve for PPV and NPV.
[Caption] Binary classification outcome chart otherwise known as a confusion matrix. From four outcomes (true positive, true negative, false positive, false negative), there are four conditional probabilities (positive predictive value, negative predictive value, sensitivity, and specificity).
| Probability given | Condition | Metric | Conditional probability notation |
|---|---|---|---|
| Odds the patient has the disease given | Test is positive | Positive predictive value | \(\text{PPV}= \text{Pr}\left( D{+}|T{+}\right) \) |
| Odds the patient does not have the disease given | Test is negative | Negative predictive value | \(\text{NPV}= \text{Pr}\left( D{-}|T{-}\right) \) |
| Odds the test is positive given | Patient is positive | Sensitivity | \( S_n =\text{Pr}\left( T{+}|D{+}\right) \) |
| Odds the test is negative given | Patient is negative | Specificity | \( S_p = \text{Pr}\left( T{-}|D{-}\right) \) |
| Positive likelihood ratio | \(LR{+} = \frac{\text{Pr}\left( T{+}|D{+}\right)}{\text{Pr}\left( T{+}|D{-}\right)} \) | ||
| Negative likelihood ratio | \(LR{-} = \frac{\text{Pr}\left( T{-}|D{+}\right)}{\text{Pr}\left( T{-}|D{-}\right)} \) |
[Caption] Conditional probability table. This table summarizes the six metrics discussed in this article. Likelihood ratios are ratios of two conditional probabilities as discussed below.
From the specificity, sensitivity, and prevalence, we can find the probability of each of the four binary classification outcomes. First, we need to recognize that the sum of all four outcome probabilities is 1.
The definition of the prevalence is
The sensitivity gives us a solution for the true positive and false negative quadrants.
The specificity and prevalence give us expressions for the false positive and true negative quadrants.
In summary, the probability of each outcome in a binary classification given a test's specificity, sensitivity, and prevalence is as given below.
| Outcome | Probability |
|---|---|
| \(T_p\) | \(S_n P_\text{prev}\) |
| \(F_n\) | \(( 1 - S_n ) P_\text{prev}\) |
| \(T_n\) | \(S_p ( 1 - P_\text{prev} )\) |
| \(F_p\) | \((1- S_p) ( 1 - P_\text{prev} ) \) |
Sensitivity and specificity are important test-performance metrics but in a clinical setting, the relevant conditional probability is based on the test result, not the disease state. Therefore, the clinician and the patient are concerned with positive and negative predictive values. By solving for PPV and NPV in terms of sensitivity, specificity, and prevalence, we discover the positive (\(\text{LR}{+}\)) and negative (\(\text{LR}{-}\)) likelihood ratios as the collection of factors that do not depend on prevalence. The positive and negative likelihood ratios are defined as \(\frac{S_n}{1- S_p}\) and \( \frac{ 1 - S_n }{S_p}\), respectively. Unfortunately, the conventional definition of the likelihood ratio is the reciprocal of the relevant term here. In the following section, we will be discussing \(\left( \text{LR}{+} \right)^{-1}\), \(\text{LR}{-}\), and their relationship to PPV/NPV.
\(\left(\text{LR}{+}\right)^{-1}\) and \(\text{LR}{-}\) contain all of the prevalence independent terms. The likelyhood ratios define the shape of the predictive value vs prevalence curves. Both terms are bounded between \(0\) (a perfect test) and \(\infty\) (a perfectly wrong test, every answer is wrong 100% of the time). In the middle, a test could have a \(\text{LR}{+}\) or \(\text{LR}{-}\) of 1 where a negative or positive result indicates the patient is just as likely to have the disease as a random member of the population. Such a test is exactly worthless since you know just as much about the odds the patient has a disease as you did before you ran the test. \(\left(\text{LR}{+}\right)^{-1}\) or \(\text{LR}{-}\) greater than 1 indicates that the test would be more accurate (regardless of prevalence) if the results were inverted. The plots below only show \(\left(\text{LR}{+}\right)^{-1}\) or \(\text{LR}{-}\) from 0 to 1 for this reason.
[Caption] Positive and negative predictive values as a function of disease prevalence. For small \(\left(\text{LR}{+}\right)^{-1}\) (good test), the positive predictive value is high regardless of prevalence; as \(\left(\text{LR}{+}\right)^{-1}\) increases the positive predictive value drops. However, if the disease prevalence is high, the positive predictive value is less sensitive to \(\left(\text{LR}{+}\right)^{-1}\). For small \(\text{LR}{-}\) (good test), the negative predictive value is high regardless of prevalence, as \(\text{LR}{-}\) increases the negative predictive value drops. However, if the disease prevalence is low, the positive predictive value is less sensitive to \(\text{LR}{-}\).
When the prevalence of a disease is low (ie all of the STDs except HSV), the positive predictive value of a test drops even if it has high specificity and sensitivity. The negative predictive value remains high. Therefore, for rare diseases, a false positive is more likely than a false negative. When a test is relatively good (high sensitivity and specificity), the positive predictive value is mostly a function of specificity and prevalence while the negative predictive value is mostly a function of sensitivity and prevalence. To properly interpret test results, all of those values and interdependent relationships must be understood.
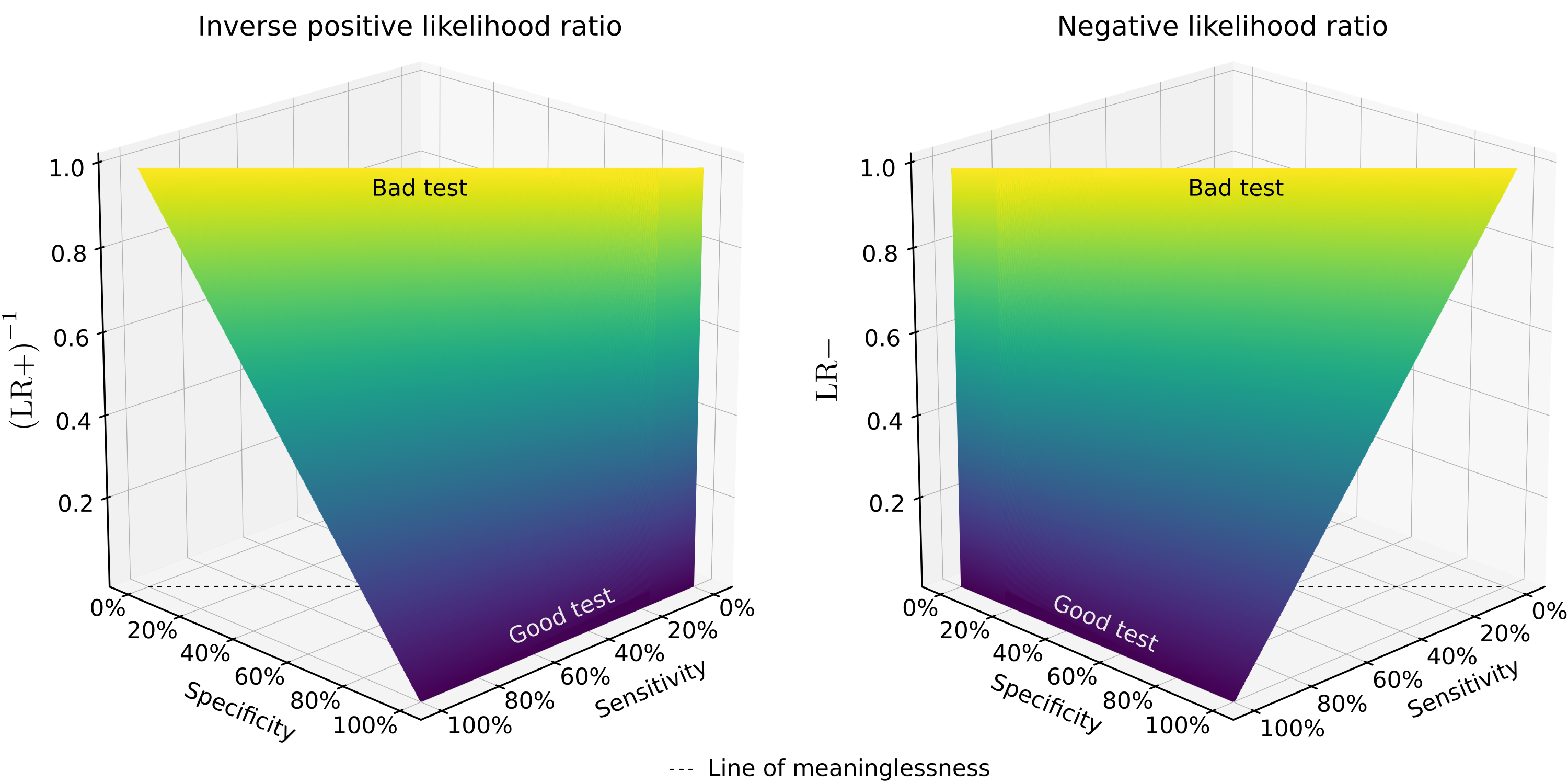
[Caption] Plots of \(\text{LR}{-} = \frac{ 1 - S_n }{S_p} \) and \(\left( \text{LR}{+} \right)^{-1} = \frac{1- S_p}{S_n}\). The likelyhood ratios define the shape of the NPV vs prevalence and PPV vs prevalence curves. At the top of the graphs where \( S_p+S_n=1\), the positive and negative likelyhood ratios are 1 (\(\text{LR}{+}=\text{LR}{-}=1\)). Along that line, the test result is exactly worthless since the patient is no more or less likely to have the disease (regardless of the type of result or prevalence) than a random member of the public. This is the "line of meaninglessness." Any test whose specificity and sensitivity sum to 1 is a test that provides no information. A tested person is just as likely to have the disease as a random member of the population.
If the test result is negative, the result is most trustworthy when the test is sensitive and the disease is low prevalence. Because all STDs are low prevalence (except herpes), a negative test result is almost always true; false negatives are rare. If the test result is positive, the result is most trustworthy when the test is specific and the disease prevalence is high. Therefore, positive STD results can only be taken seriously when the test is highly specific. This is why positive STD tests generally require a more expensive follow-up confirmation test.
Enter values between greater than 0 and less than 1 or 100%. Values equal to 0, 1, or 100% will result in 'Not valid Number' or NvN as the output.
| Pathogen/test | Sensitivity | Specificity |
|---|---|---|
| HIV EIA | 99.7% [14] | 98.5% [14] |
| HIV ELISA | 94-100% [14] | >99% [14] |
| Trichomoniasis NAAT | 88-100% [15] | 98-100% [15] |
| Chlamydia NAAT | >90% [16] | >99% [16] |
| Gonorrhea NAAT | 98% [17] | 98-100% [17] |
| Syphilis ICS | 94% [18] | 93% [18] |
| HSV ELISA | 97-100% [19] | 94-98% [19] |
[Caption] These figures are ranges or estimates. Most come from review papers which are careful to hedge their claims - "at least 2 large studies found sensitivities of 94-99%." Test performance varies over time as we learn by collecting more data. As technology and research march on, test performances improve and this section will rapidly be out of date. With that in mind, I strongly recommend you compute the PPV/NPV of every screening test (STD or otherwise) you take. Demand your clinician tell you the sensitivity/specificity of every screening test he/she orders. Find the current prevalence data from the CDC's website using your geographic location, gender, etc. Compute the positive and negative predictive values as described above. In an ideal world, this would be widely regarded as an obligation of the medical community. I have not computed the PPV/NPV of these tests based on modern prevalence data for two reasons. (1) It will rapidly be out of date as disease prevalences change with time and (2) the sensitivity/specificity data reported here do not necessarily apply to your tests. As technology and research march on, and as diseases develop new strains, these numbers will vary. To be an informed healthcare consumer, you need to know the sensitivity and specificity of the medical exams you are subjected to.
Some medical exams, mostly physical exams and not lab findings, are astonishingly bad. For example, Homans' sign is a test for deep vein thrombosis (DVT) which is neither specific nor sensitive. Pain behind the knee during forced dorsiflexion of the foot as an indication of DVT was first described by Dr. John Homans in 1934 [20]. It is so unreliable and practiced so widely that the medical community has resorted to citing its historical value as a reason to continue practicing it [21]. Dr. Homans died in 1954 but even by that time, the uselessness of his eponymous sign was well known to the wider community and to himself [22]. Homans' sign has a sensitivity and specificity of 8-56% and <50%, respectively [23]. This means that if Homans' sign is positive, you are less likely to have DVT than a random member of the public, if it is negative, you are more likely than a random person to have DVT. The test is more accurate if you invert the findings though not accurate enough to be of any utility. It is worse than useless because it deceives clinicians into thinking they have actionable information when they absolutely do not.
The moral of the story is "just because your doctor does it, does not mean it is a useful thing to be doing." Homan's sign is one of many medical practices that remind us of the need to be informed, critical, and involved patients. In fairness to the medical profession, this particular test is no longer taught to new doctors. In fairness to the rest of us, it is still a topic of contention in some parts of the medical field and there is no excuse for that.
[1] "Human Chorionic Gonadotropin (HCG)," StatPearls [Internet], 2019.
[2] "Detection of early pregnancy forms of human chorionic gonadotropin by home pregnancy test devices," Clinical Chemistry, vol. 47, pp. 2131—2136, 2001.
[3] "A new reference preparation of human chorionic gonadotrophin and its subunits," Bulletin of the World Health Organization, vol. 54, pp. 463, 1976.
[4] "Hepatitis Viruses," in Transfusion Microbiology, pp. 9—23, 2008.
[5] "Acquired immunodeficiency in an infant: possible transmission by means of blood products," The Lancet, vol. 321, pp. 956—958, 1983.
[6] "Pneumocystis Pneumonia - Los Angeles," Morbidity and Mortality Weekly Report, vol. 30, pp. 250—252, 1981.
[7] "Reduction of the HIV seroconversion window period and false positive rate by using ADVIA Centaur HIV antigen/antibody combo assay," Annals of Laboratory Medicine, vol. 33, pp. 420—425, 2013.
[8] "Detection of acute HIV infection: we can't close the window," Journal of Infectious Diseases, vol. 205, pp. 521—524, 2011.
[9] "An Overview of Enzyme Immunoassay: The Test Generation Assay in HIV/AIDS Testing," Journal of AIDS & Clinical Research, vol. 9, pp. 2, 2018.
[10] "Diagnostic tests for sexually transmitted infections," Medicine, vol. 46, pp. 277—282, 2018.
[11] "Risk of window period HIV infection in high infectious risk donors: systematic review and meta-analysis," American Journal of Transplantation, vol. 11, pp. 1176—1187, 2011.
[12] "Time periods of interest - HIV, STDs, Viral Hepatitis," 2018.
[13] "Timing of chlamydia tests," Sexually Transmitted Infections, 2008.
[14] "Screening for HIV: a review of the evidence for the US Preventive Services Task Force," Annals of Internal Medicine, vol. 143, pp. 55—73, 2005.
[15] "Modern diagnosis of Trichomonas vaginalis infection," Sexually Transmitted Infections, vol. 89, pp. 434—438, 2013.
[16] "Review of Chlamydia trachomatis viability methods: assessing the clinical diagnostic impact of NAAT positive results," Expert Review of Molecular Diagnostics, vol. 18, pp. 739—747, 2018.
[17] "Self-collected versus clinician-collected sampling for chlamydia and gonorrhea screening: A systemic review and meta-analysis," PLoS One, vol. 10, pp. e0132776, 2015.
[18] "Field evaluation of simple rapid tests in the diagnosis of syphilis," International Journal of STD & AIDS, vol. 19, pp. 316—320, 2008.
[19] "Diagnosis of genital herpes simplex virus infection in the clinical laboratory," Virology Journal, vol. 11, pp. 83, 2014.
[20] "Thrombosis of the deep veins of the lower leg, causing pulmonary embolism," New England Journal of Medicine, vol. 211, pp. 993—997, 1934.
[21] "Homan's sign for deep vein thrombosis: A grain of salt?" Indian Heart Journal, vol. 69, pp. 418, 2017.
[22] "John Homans, MD, 1877-1954," Archives of Surgery, vol. 134, pp. 1019—1020, 1999.
[23] "Beauty is in the eye of the examiner: reaching agreement about physical signs and their value," Internal Medicine Journal, vol. 35, pp. 178—187, 2005.