
Photo credit to Keith Johnston
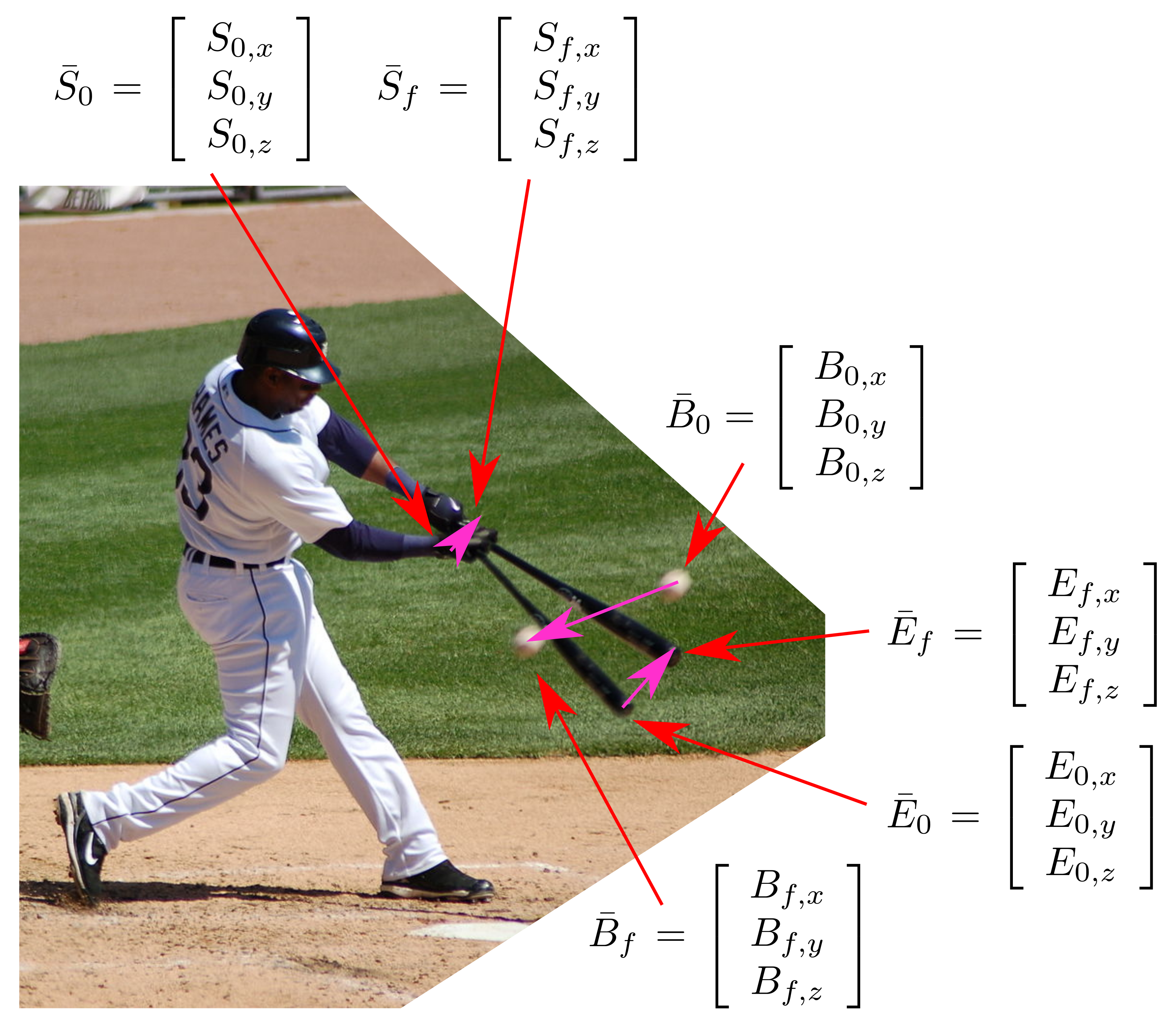
In 2016, a friend asked me for help with a virtual reality problem. He was trying to find the collision in space between a baseball and a bat between frames of a physics simulator for a VR system. If you want to build VR software that can train professional athletes, accuracy is important.
The obvious approach, the one I thought of first, is a numerical solution but it is too slow. My desktop took 100-300 ms to solve it numerically but we only have 30 ms between frames if we have a 30 hz frame rate. The code below solves the problem explicitly in roughly 10-20 µs. What starts as an 18 variable algebra problem can be reduced to the roots of a 4th order polynomial. It just takes several pages of algebra.
The code below is confusing. I cannot understand why it works without seeing the derivation and I doubt anyone could. To understand why it works, see the documentation.
import matplotlib.pyplot as plt
import numpy as np
# Bat start and end positions are given as 2 tuples of x,y coordinates,
# the first tuple is the knob of the bat handle, the second is the end of the fat end of the bat
# the ball is defined by 1 tuple of x,y coordinates at the center
bat_start = ((0,0,0),(-1,5,0))
bat_end = ((1,0,0),(2,5,0))
ball_start = (30, 3.5, -10)
ball_end = (-10, 3.5, -10)
frame_length = 16.66 #ms 1/60*1000 frame length @ 60 Hz
ball_r,bat_r = [2.5,2.5]
# point = np.array(x,y,z)
# line = [np.array(x,y,z),np.array(x,y,z)]
def separation(point,line,inv =1):
lin_interp = lambda v1,v2,t: v1+(v2-v1)*t
v = (lambda t: lin_interp(i,j,t) for i,j in zip(line[0],line[1]))
tt = -np.dot((line[0]-point),(line[1]-line[0]))/np.dot((line[0]-line[1]),(line[0]-line[1]))
V = np.array([j(tt) for j in v])
d = np.sum((V-point)**2)**.5+inv*(bat_r+ball_r)
d_raw = np.sum(V-point)
return d,d_raw
def vec_interp(p1,p2):
return lambda t: (p2-p1)*t/frame_length+p1
def path_trace_min(bat_start,bat_end,ball_start,ball_end,show = False):
bat_start = [np.array(i) for i in bat_start]
bat_end = [np.array(i) for i in bat_end]
ball = [np.array(i) for i in [ball_start,ball_end]]
dE = vec_interp(bat_start[1],bat_end[1])
dS = vec_interp(bat_start[0],bat_end[0])
dB = vec_interp(ball[0],ball[1])
tt = np.linspace(0,frame_length,300)
inv = -1 if separation(dB(i),[dS(i),dE(i)])[1]<0 else 1
d = [separation(dB(i),[dS(i),dE(i)],inv)[0] for i in tt]
dr = [separation(dB(i),[dS(i),dE(i)])[1] for i in tt]
D = lambda i: separation(dB(i),[dS(i),dE(i)],inv)[1]
# find t, collision time
# print np.where(np.array(d)<0)[0]
if len(np.where(np.array(d)<0)[0])>1:
p2 = d[np.where(np.array(d)<0)[0][0]]
t = tt[np.where(np.array(d)<0)[0][0]]
print [t,p2]
else:
t=0;p2=10
if show:
plt.plot(tt,d); plt.legend();
plt.title('distance vs time'); plt.xlabel('time');
plt.ylabel('distance between ball and bat')
plt.plot(tt,dr);plt.show()
return t,dB,dS,dE,p2